6.c) Esnuka billiards and genetic algorithms of the Global Model of simulation
After introducing into the Social Model the functional limitations due to genetic problems and quantitative variables with random disturbances similar to the variables of observed data; the genetic inheritance of intelligence or Global Model works satisfactorily as the images associated with the following tables show.
Billiards evolutionary game
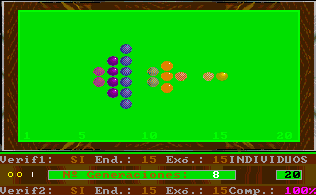
The third surprise was that the complete model contains the same parameters as the billiards game Esnuka (1992) about the genetic problems regarding the nature of intelligence. Some of those problems were not in the initial model to simplify both its presentation and the statistical study.
There is no need for either a simulation or the generation of the objective function R if the adjustments operate directly on M (mothers) and F (Fathers) to prove the innate nature of intelligence and the presence of the LoVeInf method.
The game Esnuka is a billiards program in which the colors of the balls depend on evolutionary states grounded on the obtained cannons, in agreement with the postulates of the Conditional Evolution of Life (CEL). The simulation game Esnuka does not require so many random variables because the computer does not produce errors in the IQ expression or the measurement, and the changing colors of the balls take place with a chosen constant percentage from the options panel.
All the following graphs relate to the Global Model with functional limitations and 5% of internal evolution. Of course, to obtain a suitable optical effect of the graphs, they are the W showing better adjustments to one of the C variables of the children.
6.c.1) Original variables
The original individual variables do not always improve their adjustment within the statistical simulation of the Global Model, whereas the centered variables do. For rearrangement criterion (M+F)/2, it is obvious because this criterion does not respond to changes in the parameters of internal evolution.
5% internal evolution
Intelligent test of Wechsler and Stanford-Binet scales
| Order | Objective function | |||||
| R° | M & F | |||||
| Graphs | GMCI | r² max. | Graphs | GMCI | r² max. | |
| (M+F)/2 | q051° | 11,73 | 0,62 | q052 | 13,05 | 0,80 |
| M1F1° | q053° | 10,91 | 0,79 | q054° | 13,04 | 0,79 |
| R° | q055° | 10,83 | 0,73 | q056° | 12,63 | 0,94 |
| WB | q057° | 12,26 | 0,89 | q058 | 14,68 | 0,99 |
| ° Internal evolution parameters affect the objective function R and M1F1 order | ||||||
A graph could only change with the evolution parameters when either the objective function or the rearrangement criterion varies because because the C variables of the children, mothers M and fathers F are observational. When values are affected, the variables concerned have a circle in their names; therefore, when the column or row headings of next tables have a (°), it indicates that the model adjustment has changed due to the evolution parameters.
Admittedly, the model could be more precise, but its main structure is valid. In addition, it could be that the original variables, with so many deviations and despite the sensitivity of the Global Model with its random variables, are not capable of detecting the limited effect of the internal evolution parameters.
It is too soon to make definite conclusions; for example, sometimes the three C variables behave similarly and sometimes very differently. It is possible the different IQ tests measure distinctive abilities and, therefore, responding differently when the perspective of the analysis changes.
The perception of the quantitative analysis of the Global Model is far more profound than just an IQ test alone.
In other words, it could be certain elementary functions of intelligence belong to a hard nucleus not usually affected by the internal evolution of a single generation. Confidently, a minimum human IQ would improve the goodness-of-fit of the model; in particular, this minimum could be around an IQ of 50 or 60 points, although there will always be exceptions by severe cerebral alterations of some individuals.
Even so, the correlations obtained with the individual variables are 0.89 for function R° –defined by the CEL– and of 0.99 for M & F. This last result, however, is the same as with the model without evolution because the evolution do not alters M & F or the criterion of arrangement WB.
Also, variable R° as an arrangement criterion allows a correlation of 0.94, which is excellent, and 0.79 for both objective functions when the order is M1F1°.
Of course, the behavior of variable W° is impressive in all of them. Undoubtedly, the visual effect of the graphs accounts for the high-quality specifications of the Global Model.
6.c.2. Centered variables
Centered variables maintain a better adjustment than original ones.
The graphs of the Global Model speak for themselves.
| Order | Objective function | |||||
| R° | M & F | |||||
| Graphs | GMCI | r² max. | Graphs | GMCI | r² max. | |
| (M+F)/2 | q061° | 14,70 | 0,77 | q062 | 16,03 | 0,80 |
| M1F1° | q063° | 15,61 | 0,89 | q064° | 17,77 | 0,89 |
| R° | q065° | 15,55 | 0,84 | q066° | 17,40 | 0,97 |
| X6 | q067° | 15,05 | 0,91 | q068 | 17,20 | 0,88 |
| ° Internal evolution parameters affect the objective function R and M1F1 order | ||||||
In comparison to the centered variables without internal evolution, the GMCI increases more with the objective function M & F than with R°; although it is significant in both cases. Besides, the GMCI increment is higher with criterion M1F1° than with R°, with 1.70 and 1.52 points respectively.
For both objective functions R° and M & F, the results progress with the arrangement criteria R° and M1P1°.
