5. The Social Model of the evolution of intelligence
5.a) Statistical data of homogenous groups
The weak adjustment obtained in the previous section was foreseeable; the initial specifications of the model included that the proposed estimator would be unbiased and its variance enormous due to the random character of the Mendelian inheritance.
In addition, it indicated the impossibility of correcting the problem of the statistical data by selecting 50% of the sample where the deviations would have to be minimum. Lack of precision in measurements and temporary and functional variations of the intelligence expression are the leading causes. The issue with the statistical data is higher than expected.
The analysis by groups seemed the only way to surpass the limitations of the available statistical data. The Social Model makes different size groups with the various rearrange orders of the initial seventy values.
The aggregation without reorder would not be satisfactory since the values of all the variables would tend towards the average as the group's elements increase.
Reorganizing the initial sample with criteria such as *M1F1 or *(M+F)/2, it will be possible to achieve homogenous groups in which:
The effectiveness of the previously mentioned compensations will be optimum.
The groups divided in stratums will allow for a suitable adjustment of the tendency or relation between the variables of the model.
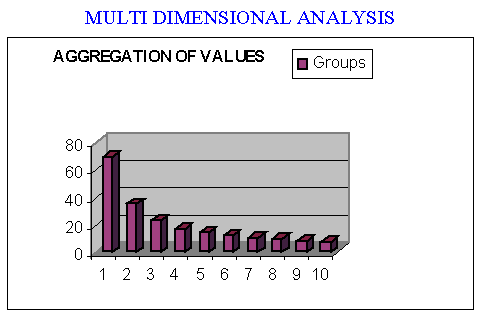
For each variable, the model uses a hundred and ten generated variables based on the diverse number of elements and criterion to the group's rearrangement; there are ten group sizes and eleven modes of the arrangement, including the initial order, which is unknown.
correlational research
The variables to rearrange the groups are M, F, R, M1F1, (M+F)/2, 2F2M, C1, C2, C3, and W. Variable 2F2M will be opposed to M1F1 conceptually; C variables correspond to the children of a particular analysis and W variables appear in the model simulations artificially.
The image shows the design of grouping the elements of the sample to compensate for the deviations due to measurement errors and the genetic combination.
The graph contains the number of elements of the sample for each group size.
The Social model has a double formulation, on the one hand, calculating the correlation of children C vectors with respect to the objective function R, determined in accordance with the Conditional Evolution of Life (CEL). On the other hand, with respect to the variables of the statistical data M and F directly, allowing for a comparative analysis between the two formulations.
The final effect is that the statistical data evaluated by the model about the nature of intelligence has multiplied several times over and random variations have compensated. Consequently, its power to detect the correction of its specifications has improved significantly. At the same time, the model of evolution of intelligence has become very sensitive and can compare between close configurations of the statistical data.
5.b) Quantitative approach
The Social Model aims to verify innate engineering in the evolution of intelligence according to the Global Cognitive Theory.
The main conclusion of the model with grouping, Mendelian genetics, and the Conditional Evolution of Life (CEL) is the confirmation of the goodness of the adjustments by grouping the values and their prior arrangement. The correlations achieved, despite the limitations of the available information, allow affirming that the characteristics collected by the intelligence tests transmit from one generation to another fundamentally.
The results are surprising regarding the nature of intelligence, which can be observed both in the graphs of the statistical annex and in the following tables. An aspect that will allow reaching some crucial conclusions is the model sensitivity of the arrangement criterion.
Indeed, this model offers an almost instantaneous perception of the exactitude of a specification; sixty coefficients of determination (r²) highlights the global and underlying relations of the involved statistical data for each case.
The considerable increase of the correlation between homogenous groups of the statistical data is not due to the reduction from 68 to 5 or 4 degrees of freedom, since the results with non-homogenous groups, without previous rearrangement, have the same degrees of freedom and the correlation even lowers for the sample without grouping.
The Social Model provides a double formulation; on the one hand, the statistical analysis of the IQs of the children on the Wechsler and Stanford-Binet scale concerning the objective function R determined according to the CEL and the Mendelian genetics. On the other hand, the correlations between the IQs of the children versus the mothers (M) and the fathers (F) directly, permitting a comparative analysis. In the latter case, the multiple regression use the method of ordinary least squares.
Likewise, for both formulations, there are four statistical criteria of the prior ordering of values corresponding to the variables marked with (*)
5.b.1) Stanford Binet and Wechsler IQ test
The Social Model adjusts perfectly, showing a determination coefficient r² superior to 0.9 in several cases.
Moreover, it is interesting that the objective function R is almost as powerful as variables of mothers M and fathers F together.
As for the statistical criteria of ordering (*), the best one is variable WB, and the variables (M+P)/2, M1P1, and R are similar.
The estimated correlations to variables M and F of r² are of 0.99 for variable WB (Wechsler intelligence test) when the rearrangement variable is the same *WB variable. This impressive outcome is possible because, in their configuration, the children variables C not only incorporate criterion *M1F1 but the real information of the power of all the genes and their correct Mendelian inheritance combination, in agreement with the CEL.
Variables *M1F1 and *R only incorporate, so far, a partial effect which is the Mendelian inheritance and, therefore, variable *WB (Wechsler intelligence test) is a better order criterion.
Nevertheless, this does not take place in all cases; it is a consequence of the incorporation of the differences due to the expression and measurement of the IQ in C variables, which does not happen with variables *M1F1 and *R.
The table shows the G-MCI (Global Multidimensional Correlation Index) and the maximum r² of the correlations between the IQ of the parents (M & F) or vector R, and the children's IQ rearranged in four criteria. The C variables are original ones with no change in any of their values.
Also, when the model has more freedom with the two variables, M and F, it adjusts better by statistical effect, or just the available data.
This table helps to understand the irregular relation between the maximum r² and the G-MCI.
One unusual aspect not delved into the analysis is the different outline of the graphs without prior order, the T4 and the WB on the one hand and the T1 on the other. The correlations of the latter show the typical teeth shape of the ordered values more clearly but without the upward trend.
The variable T1 may have a deviation not included in the model. It should be random because it mostly compensates and, at the same time, is independent of the value of the intelligence coefficients. Perhaps it is due to the young age of the children when performing the test.
This deviation occurs for correlations with both the R function and M & F as explanatory variables. Although, in the second case, the compensation is more exact and could indicate that somehow information regarding this deviation vanishes when generating the R function from the M & F variables.
5.b.2) Centered or average variables (Combination of Stanford Binet and Wechsler IQ test)
Centered or average variables incorporate some correction in their values, either of the extremes values or for being average of other variables Wechsler and Stanford-Binet test, such as the children variables T1-d, the X3, and the X6.
As expected, the compensation of random deviations in the values of the centered variables makes the new statistical analysis fit significantly better than the model with original vectors. Besides, the more focused the variable, the better fit it provides in almost all cases.
In the eight graphs of this model, the Global Multidimensional Correlation Index (GMCI) is superior to the maximum GMCI of the model with original IQ variables.
Regarding the coefficients of determination r², there are values of 0.79 or higher in all the graphs of the model.
Due to the higher coefficients of determination r² of each graph, on the one hand, the goal variable R exceeds the variables M & F together with the sorting criteria *X6 and, on the other hand, that the sorting criteria *M1F1 is higher than *WB.
It is interesting to note that the goal function R is almost as powerful as the M & F variables together, reaching similar values to the highest coefficients of determination r² of each graph.
As for the sorting criteria (*), the four variables (M+P)/2, M1P1, R, and X6 are similar. The variable X6 stands out for the GMCI with the M & F as explanatory variables and the (M+F)/2 with the R function.
Now, paying attention to the graphs of the centered variables, T1-d, X3, and X6, in the first place, the q23 has a singular beauty because of its shape and content.
This graph shows an increase of correlation with the R aim function proposed by the general theory of Conditional Evolution of Life (CEL) regarding the nature of intelligence, until it surpasses 0,9 (GMCI = 14.98), as the other correlation vectors involved a move to more centered values.
After all, the variables are not as off as they seemed at the beginning. In particular, the result of the quantitative approach is coherent with the supposition that these centered variables should have fewer problems with the variability in the expression and measurement of the intelligence quotients, since, by definition, they imply a compensation of those deviations.
On the other hand, bearing in mind the parallelism between the variables T1-d, X3, and X6 and the upright correlations that they provide, it was a reasonable assumption to generate variable T1-d with a 10% maximum margin of variation to the average in variable T1 (Stanford Binet IQ test). However, it makes sense the results are not as virtuous as the X3 and X6 variables.
Another element to point out is the effectiveness of the employed multidimensional analysis. It lets us to draw quickly some conclusions while maintaining a high degree of coherence and security in the reasoning.
The groups have a maximum of ten elements, and due to the observed tendency, with groups of 20, the correlation will be more significant.
It seems there is not much margin left to deny the hereditary nature of intelligence, not even to try to reduce it to less than 80%.
