5. Modello di dati dell'Intelligenza Sociale
5.a) Criterio statistico d'ordine delle variabili in gruppi omogenei
Il debole adattamento ottenuto nella ricerca quantitativa della sezione precedente era prevedibile; era già stato detto nelle specificazioni iniziali del modello statistico che lo stimatore proposto sarebbe stato uno stimatore corretto, ma che la sua varianza sarebbe stata molto grande per il carattere aleatorio della combinazione genetica mendeliana.
È inoltre stata menzionata l'impossibilità di correggere questo problema selezionando solo il 50% del campione, dove le deviazioni dovrebbero essere minime, per la mancanza di precisione delle misurazioni realizzate e della stessa espressione temporale e funzionale dell'intelligenza. Il problema dello studio correlazionale è di una portata più grande di quanto si pensi.
Un modo per ovviare questi limiti del metodo correlazionale è stato l'aggruppamento degli elementi del campione, configurando ciò che potremmo definire intelligenza sociale o di gruppi, in modo tale che nei nuovi elementi vengano compensate le differenze dovute sia a possibili errori di misurazione che alla varianti o differenze generate dalla combinazione genetica.
Questo raggruppamento dei dati della ricerca quantitativa non sarebbe di per sé sufficiente, poiché i valori di tutte le variabili generate tenderebbero alla media della popolazione totale, formando gruppi più grandi.
Prima del raggruppamento si deve procedere ad un riassetto del campione in funzione di qualche variabile o criterio statistico come M1P1 o (M+P)/2, allo scopo di ottenere uno studio correlazionale di gruppi omogenei che:
- Massimizzino l'efficacia di tali compensazioni.
- Si differenzino fra di loro con la maggior chiarezza possibile per poter permettere un adattamento corretto della tendenza o proporzione dell'intelligenza del gruppo o intelligenza sociale fra le variabili del modello.
Per ogni variabile sono state generate 110 diverse variabili in funzione della distinta aggregazione effettuata; ovvero, dieci raggruppamenti diversi con undici criteri statistici d'ordine delle variabili studiate, fra le quali comprendiamo l'ordine iniziale fornito dai dati dello Young Adulthood Study, cioè senz’ordine noto.
Le variabili scelte nel disegno dello studio correlazionale come criteri statistici d'ordine di valori sono state M, P, R, M1P1, (M+P)/2, 2P2M, F1, F2, F3 e W; intendendo con variabili F quelle dei figli oggetto di studio in un’analisi particolare. La variabile 2P2M sarà concettualmente opposta a M1P1 e W le variabili generate artificialmente nella simulazione del modello.
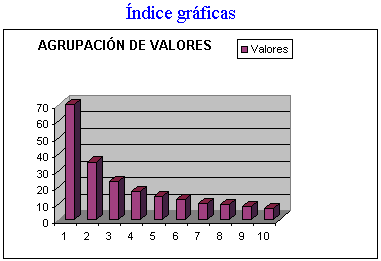
Disegno dei quadri statistici della ricerca quantitativa con raggruppamento di elementi del campione per compensare le differenze risultate di errori di misurazione e di variazioni o differenze provocate dalla combinazione genetica.
Il grafico contiene il numero di valori del campione che esisterà per ogni dimensione del gruppo.
Le stime ottenute con questo disegno correlazionale con gruppi grandi tenderanno ad essere più stabili perché hanno valori incorporati e perché sono più centrali, hanno, infatti, molte possibilità che le differenze si compensino internamente. Ma, allo stesso tempo, saranno più sensibili a causa del numero ridotto di valori impiegato per le stime e per la diversa ubicazione di valori estremi.
Ad ogni modo, ciò che si consegue è un’analisi multipla nelle diverse dimensioni in cui viene eseguita. Ciò permetterà di esaminare ed eventualmente di comprendere la coerenza dei risultati.
5.b) Ricerca quantitativa
Modello di dati statistici per verificare l'esistenza di un’ingegneria genetica naturale nell'evoluzione dell'intelligenza in base alla Teoria Cognitiva Globale.
La principale conclusione della ricerca quantitativa di quozienti intellettuali della scala Wechsler e Stanford-Binet sull'importanza della genetica evolutiva dell'intelligenza, nel modello con genetica mendeliana e con la Teoria Generale dell'Evoluzione Condizionata della Vita, è la conferma della bontà degli adattamenti per raggruppamento dei valori e per il loro ordine previo. Le correlazioni raggiunte, nonostante i limiti dell'informazione disponibile, consentono di affermare che le caratteristiche raccolte dai test d'intelligenza sono fondamentalmente trasmesse da una generazione all'altra.
Come si può osservare sia nei grafici che nei quadri riepilogativi della ricerca quantitativa, i risultati sono piuttosto sorprendenti. Soprattutto la sensibilità del Modello dell'Intelligenza Sociale al criterio statistico d'ordine, aspetto che ci permetterà di giungere a conclusioni rilevanti.
Il notevole incremento della correlazione per la stima con gruppi omogenei non si può imputare al calo da 68 a 5 o 4 gradi di libertà, dato che la stima con gruppi non omogenei o senza riassetto previo ha gli stessi gradi di libertà e la correlazione diminuisce addirittura rispetto al campione non raggruppato.
Il Modello di dati dell'Intelligenza Sociale è stato esaminato nella sua doppia formulazione, da una parte l'analisi statistica dei QI dei figli sulla scala Wechsler e Stanford-Binet rispetto alla funzione obiettivo R determinata in base alla ECV e alla genetica mendeliana, e dall'altro la ricerca quantitativa dei QI dei figli rispetto alle variabili di QI delle madri (M) e dei padri (P) direttamente, per permettere un’analisi comparativa per il caso della genetica umana. In quest’ultimo caso la stima della regressione multipla è stata effettuata con il metodo dei minimi quadrati ordinari.
Inoltre, per entrambe le formulazioni sono stati utilizzati quattro criteri statistici di ordine previo di valori corrispondenti alle variabili contrassegnate con (*).
5.b.1. Variabili originali - Wechsler e Stanford-Binet test
L'effetto della riformulazione del Modello Individuale è chiaramente osservabile, il nuovo modello di ricerca quantitativa di genetica evolutiva con coefficienti d'intelligenza si adatta perfettamente, giungendo ad un r² superiore allo 0,9 in diversi casi.
In più, è interessante comprovare che la funzione obiettivo R, proposta dalla Teoria Generale dell'Evoluzione Condizionata della Vita, è quasi così potente come le variabili M e P insieme.
Per quanto riguarda i criteri statistici d'ordine (*), le variabili (M+P)/2, M1P1 e R si rivelano simili, particolarmente la variabile WB quando è utilizzata come criterio d'ordine.
Se eseguiamo una stima in funzione a M e P, l'r² ottenuto arriva allo 0,99 per la variabile T1 quando il criterio statistico d'ordine previo è la variabile WB. È possibile che sia dovuto al fatto che questa variabile incorpora tutti gli effetti coinvolti nella generazione naturale dei coefficienti osservati.
Le variabili M1P1 e R incorporano solo, per il momento, l'effetto di parte o di tutta la combinazione genetica mendeliana rispettivamente ed è quindi meglio la variabile finale WB.
Ciononostante, questo non avviene in tutti i casi della ricerca quantitativa. Molto probabilmente per l'incorporazione delle differenze frutto dell'espressione e della misurazione dei coefficienti F, cosa che non succede con le variabili M1P1 e R.
Inoltre, il modello di ricerca quantitativa, siccome ha più libertà con le due variabili M e P, si adatta meglio per effetto statistico, o semplicemente i dati che abbiamo a disposizione sono un caso particolare.
Occorre segnalare che questo riquadro ci aiuta ad aver un’idea della relazione esistente fra gli ICMG ed i r² massimi.
Un aspetto che non ho approfondito in quest’analisi quantitativa, che sembra interessante, è la diversa forma dei grafici dei valori senz’ordine previo. La T4 e la WB da una parte e la T1 dall'altra. Le correlazioni di questi ultimi mostrano la forma a dente di sega tipica dei valori ordinati con più chiarezza ma senza tendenza ascendente.
È come se esistesse una deviazione solo nella variabile T1 non raccolta nel modello che si compensa in gran misura e quindi dev’essere aleatoria ed al contempo è indipendente dal valore dei coefficienti d'intelligenza. Forse è dovuto alla giovane età dei figli nel momento in cui venne realizzato questo test d'intelligenza.
La suddetta deviazione avviene per le correlazioni con la funzione R come variabile esplicativa e per M & P come variabili esplicative. Tuttavia, nel secondo caso la compensazione è molto più esatta e potrebbe indicare che in qualche modo si perde informazione riguardante questa deviazione nella creazione della funzione R a partire dalle variabili M & P.
5.b.2. Variabili centrate – Analisi statistica con combinazioni di Wechsler e Stanford-Binet test
Vengono definite variabili centrate le variabili che incorporano un tipo di correzione per lo studio correlazionale, sia degli estremi che come risultati della media di altre variabili Wechsler e Stanford-Binet test, come ad esempio la T1-d, le X3 e le X6, tutte dei figli.
Come si poteva prevedere, la compensazione delle deviazioni più o meno aleatorie nei valori delle variabili centrate fa sì che la nuova analisi statistica si adatti molto meglio del modello con variabili originali. Inoltre, più è centrata la variabile e più appropriato sarà l'adattamento risultante in tutti i casi.
Grafici e statistiche
In modo tale che negli otto grafici di questo modello l'Indice di Correlazione Multidimensionale Globale (ICMG) è più alto del massimo ICMG del modello con variabili originali del quoziente intellettuale.
Per quanto riguarda i coefficienti di determinazione r² bisogna indicare che in ogni grafico del modello si ottengono valori di 0,79 o superiori.
Per i maggiori coefficienti di determinazione r² di ogni grafico, da una parte la variabile oggetto R supera le variabili M e P insieme, con il criterio d'ordine X6, e dall'altra il criterio d'ordine M1P1 è superiore al criterio WB.
È interessante constatare che la funzione obiettivo R è quasi così potente come le variabili M & P insieme, raggiungendo valori completamente simili nei coefficienti maggiori di determinazione r² di ogni grafico.
In quanto ai criteri d'ordine (*), le quattro variabili (M+P)/2, M1P1, R y X6 si rivelano simili. Si distinguono per l'ICMG la variabile X6, quando si usano le variabili M & P come variabili esplicative, e la (M+P)/2, quando la variabile esplicativa è la funzione R.
Quindi, se ci soffermiamo sui grafici delle variabili centrate della ricerca quantitativa, composte dalla T1-d, che aveva un massimo del 10% di margine d'oscillazione rispetto alla media, e dalla X3 e X6, possiamo osservare innanzitutto che il grafico q323 è di una bellezza singolare per la forma e per il contenuto.
Se cambiamo la variabile in senso da minore a maggiore centrata, questo grafico ci mostra come aumenta man mano la correlazione con la variabile R proposta dalla ECV fino a superare il 90% (ICMG = 14,98).
Dopotutto, le variabili disponibili nella ricerca quantitativa non sono così cattive come sembrava all'inizio. In concreto, il risultato è coerente con la congettura che queste variabili centrate debbano avere meno problemi con la variabilità nell'espressione della capacità intellettuale e nella misurazione dei coefficienti d'intelligenza, poiché, per il disegno stesso, sono una forma di compensazione di queste deviazioni.
D'altra parte, visto il parallelismo fra la variabile T1-d e le X3 ed X6 da un lato e le buone correlazioni che forniscono dall'altro, possiamo concludere che la correzione effettuata è un’ipotesi ragionevole, in quanto consente solo un margine del 10% rispetto alla media nella variabile T1, è un’ipotesi ragionevole. Tuttavia, non è così buona come le variabili X3 ed X6.
Un altro elemento da rilevare è l'efficacia del disegno dell'analisi multidimensionale che stiamo utilizzando, poiché ci permette di trarre alcune conclusioni con relativa facilità ed al contempo con un grado di coerenza e di sicurezza nei ragionamenti.
Occorre considerare che stiamo parlando di gruppi di dieci elementi al massimo e che per la tendenza con gruppi di 20 la correlazione sarà maggiore.
In sostanza, l'analisi statistica con variabili centrate rinforza la conclusione della ricerca quantitativa del modello con variabili originali rispetto alla trasmissione dell'intelligenza da una generazione all'altra e lascia poco margine di dubbio alla stessa, viste le elevate correlazioni risultanti.

Grafici e statistiche