2. COMPUTER SIMULATION OF EVOLUTION
Esnuka not only helps learning games of billiards, pool, and snooker but also has computer educational games of evolution with his options of simulation of evolution Esnuka-I, II, and III.
On top, Esnuka has a simulation of the evolution of the billiards balls using the CEL genetic algorithms and Mendel's laws.
To some extent, the general idea is that genetic algorithms prove the theory of Darwin, but it is far from that. If they had useful programs, it could be just the opposite because the genetics algorithms should be math functions to search for new situations with different approaching methods.
The programs need a goal or a math function to optimize within the genetic algorithms, and that is closer to a teleological or finalist evolution than Darwinian evolution.
Furthermore, as humans design these genetic algorithms, they are always the result of intelligent design.
Nevertheless, even if some genetic algorithms could be consistent with the theory of evolution of natural selection, it is clear that they do not prove it; there can be other causes of evolution working together.
Precisely, here is a specific option designed to show a fast evolution without needing to play billiards, making it easier to understand the rules behind the computer educational games of Esnuka.
Again, it may resemble a tricky understanding of the way evolution takes place in these games. However, even in the case, one does not understand the rules of the theory of evolution, will assimilate its effect intuitively.
Of course, it is advisable to read the CEL, but it is not necessary; the idea o learning while discovering the games is not a bad option. It will be much easier to comprehend the CEL afterward.
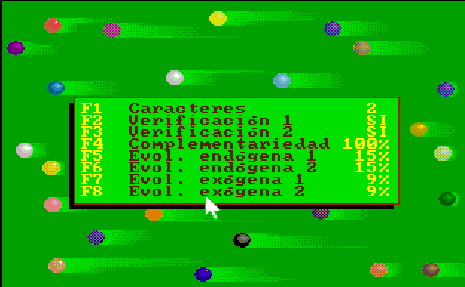
The evolutionary option of Esnuka allows the observation of the changes produced by a specific number of generations for the whole population, for 20, 30, or 100 individuals. If Sound is off, it will be 100.
The difficulty level parameter controls how to calculate the potential of genes. For difficulty levels 1 and 2, the initial values of the potential of the genes are randomly calculated within a limit of 1 to 3 and are independent of each other. Otherwise, for values 3 and 4, the potential of the genes of an individual is equal. This characteristic hardly affects the evolutionary process; however, in the latter case, the values tend to be less extreme within their range.
This option appears on the screen with two different or equal-sized circles, respectively. Nevertheless, if the color inversion function is active, all the genes will be set up with the same value, and it will show on the screen by one circle.
The difficulty level parameter also decides which simulation rules of the genetic algorithms to use under either Esnuka I for values 1 and 3 or Esnuka II for values 2 and 4. One or two vertical lines represent this on the screen.
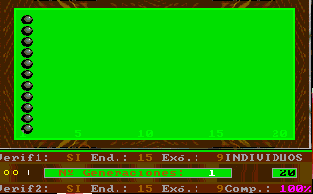
With the simulation option, a screen will appear displaying a random initial situation within a limit of 1 to 5; in other words, the left-hand side of the evolution screen. The balls will depend on the configuration of the fixed verification or complementary genetic algorithm parameters.
Pressing any key will develop a new generation according to the parameters established in the configuration menu. These parameters are always on the screen.
The detail of each evolutionary step is identical to the one used in Esnuka I and II, the rules governing the interchange of genes are Mendel's established theories, and the probabilities of transmission are equal for each gene.
In this way, the effect on the evolution of the Logical Verification of Information (LoVeInf) method and complementary character concepts are visible.
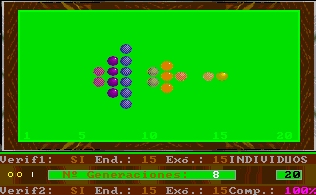
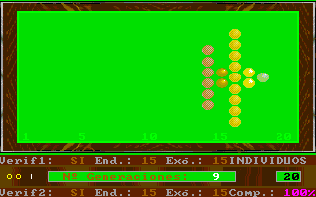
In particular, the selection of external verification means that the figures resemble the tip of an arrow; complementary genes change the shape of the figure slightly, which reminds us of fractals.
The speed of evolution depends on its parameters and is the same with or without external verification; nevertheless, the former case will be out of step compared with the latter.
Another visible effect is the increase in distance between individuals when internal evolution parameters are small compared to external evolution parameters and vice versa.
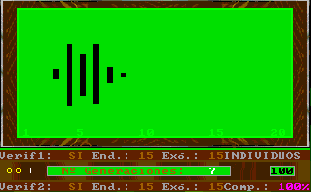
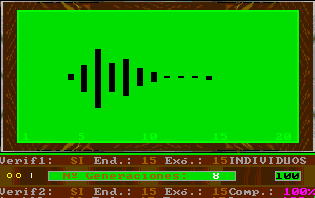
By fixing a small value to endogenous and exogenous evolutionary parameters, the program shows the behavior of evolution in the long term. It is equivalent to increasing dimensions of the evolutionary window without changing the evolutionary parameters.
Differences between consecutive colors are always constant, and endogenous and exogenous evolutionary parameters are in percentages.
As an additional explanation, colors are always in the scale 1 to 20; therefore, the potential represented by colors is the same in the cases of genes, characters and individuals, the only exception being individuals with complementary characters. For example, the potential of an individual with two complementary characters with potential equal to 10 will be ten times 10 = 100, divided by 20 = 5, to standardize the range 1 to 400.
Finally, computer educational games help to understand concepts and relations, but complex ideas need some time; it is life.
