2.c) Concept, postulates and elements of the Theory of Special Relativity
The Theory of Special Relativity put forward by Albert Einstein in 1905 discusses topics related to reference frames. Inertial reference frames are those moving at a constant velocity relating to others or the uniform relative motion.
This theory incorporated numerous ideas that were around during that time, and it discarded the existence of luminiferous aether definitively. It had various implications for the nature of light and the assumption of the relativity of time and space.
In the following section, we will briefly explain how –in addition to elements of the relativity of space and time– Einstein incorporated the novelty of the mass-energy equivalence; in other words, the concept of relativistic mass and and foundations of the atomic bomb.
The two postulates, which provide the basis for the Theory of Special Relativity, are the following:
Physical laws may be expressed by equations that have the same form for all reference frames, which move at a constant velocity with respect to each other.
The speed of light in free space takes the same value for all observers, independently of their state of movement.
One of the main criticisms is that SR is an ad hoc theory. GR subsequently had the same characteristic, as it developed to solve the insurmountable flaws of the first one, such as the paradox of the twins. Well, if GR solves this paradox is because GR only gives local solutions, so one twin cannot go too far away.
Tailored suit of mathematical interpretations
No attempt to explain the nature of the speed of light entirely stuck. Then Einstein gathered a series of known facts from the era and fit them together in a more or less coherent ensemble. The process is somewhat correct; however, according to the scientific method, it weakens a theory’s internal consistency.
A fundamental piece was Lorentz equations and their peculiar interpretation of inertial systems of reference with the maximum of speed of light c. They resolved many problems, and they were indeed convenient; so, like a good tailor, a theory was made to measure.
The first postulate of the Theory of Special Relativity refers fundamentally to “… equations which have the same form…”, moreover, the second to “The speed of light in free space takes the same value for all observers…”
The first postulate of relativity presents what Lorentz equations themselves implicate, which is that they do not change for different inertial frames of reference or observers. However, what it does change is internal variables definition, such as time, which goes from being monotonous, increasing, and exogenous function to an asymptotic and endogenous function.
The second postulate of relativity is even weaker. It says what Lorentz equations do mathematically; speed of light is always the same for any reference frame or any inertial observer.
The last thing we needed would be that after doing the asymptotic transformation, it would be different from any frame of reference! Presumably, the scientific method does not like equations conventionally forcing a result, and subsequently, many people are saying multiple experiments confirm that value.
In fact, Einstein could have said, “My theory is the Poincare postulates represented by Lorentz equations… besides, I know of the Michelson-Morley experiment.”
The rest in Einstein’s theory is the implications from the Lorentz mathematical game supported by the failure of the Michelson-Morley experiment concerning its original objective, and from the real physical existence of mass increase with velocity, relative to the natural frame of reference in an equivalent amount to which Lorentz equations imply. It happens that on the Earth, the natural reference system is Earth’s gravity field.
The first support, known before the elaboration of Special Relativity, is on section Michelson-Morley experiment.
The second one, referring to relativistic mass, was very suspicious, as stress in section Criticism of relativistic mass, as there were physical experiments, which pointed in that direction. Nevertheless, the increase in physical mass is only real when we measure the movement within the natural or privileged reference frame, as we explain in section Physics of movement with gravity of the book Physics and Global Dynamics.
Furthermore, as is also mentioned in the said book, the fact that mass increases with kinetic energy is correct, but it also affects the spatial configuration of the mass as a whole.
We will not go into technical details concerning whether mass increases –thereby literally fulfilling Newton's Second Law, and maintaining the principle of equality between inertial and gravitational mass– or whether the mass is invariant, but everything should be understood within a Lorentz adaptation.
Let us see in the following section the elements previously mentioned, as well as some relevant terminological issues from Special Relativity.
2.c.1. Frame or system of reference
Any method or mechanism for measurement needs a frame of reference, a point of origin upon which to base the different measurements. It is the way of reasoning; it is the tautological principle that all movement is relative.
This topic comes up with the problem of Classical Mechanics about Galileo’s principle of relativity from the 17th century. This stated that any mechanical experiment would have the same characteristics in a system at rest as in one that moves at a constant velocity with respect to the first.
Indeed, it is a matter of the classical concepts of force, mass, space, and time, with all the correspondent transformations when changing system or frame of reference.
The classical system worked perfectly until the appearance of electromagnetism and the nature of light, with its non-additive velocity regarding its source.
y' = y
z' = z
Of course t' = t
A spatial frame of reference has no secret; a point can be effortlessly determined within its frame of reference or changed using an adjustment of the origin of the new frame concerning the first one in each instant or moment with its relative motion.
We can easily obtain the correspondent magnitudes from one frame of reference to another using the Galileo transformations. Given two inertial frames of reference F and F’,t' = t
This equivalence of measurements is immediate and straightforward given the development of modern computers.
We may retain the same comment regarding the transformations under Einstein’s principle of relativity and the aforementioned Lorentz equations.
Inertial and non-inertial frames of reference
When frames of reference move with a constant velocity with respect to each other, they are inertial frames. Logically, if this is not the case, they are non-inertial reference frames. All non-inertial reference frames accelerate concerning each other.
In Classical Mechanics, magnitudes of force, mass, space, and time do not vary when they pass from one inertial reference frame to another; consequently, we call them Galileo invariants.
In a non-inertial reference frame, inertia does not follow the classical principles implied by the second law of Newton or Fundamental Law of Dynamics, relative to the proportionality between force and acceleration represented by the mass of a body, and the Third law of Newton or principle of action and reaction.
In a non-inertial reference frame, there will always be forces that support acceleration, and they will appear as fictitious forces –to which the principle of action and reaction do not apply.
In relativistic mechanics, the mass changes with velocity in inertial reference frames. Moreover, it changes with a simple switch to a non-inertial reference frame. A constant force does not produce a constant acceleration; this effect will be relevant when the speed becomes comparable to the speed of light, it is the effect of relativistic mass.
In the following section, we will see two conceptual errors regarding this matter.
The independence of the observer
Special Relativity is a theory pretending to simplify reality, as it states that we may express physical laws with equations that have the same form and that the speed of light in free space has the same value for all observers.
In fact, these formal propositions take on an immense complexity, so big that reality –not only its description– ends up depending on each observer. The relativity of time and space takes on a variability that affects the units of force and energy.
All measurements and units of the International System of Units (SI), also called the International System of Measurements, are dependent on the velocity and situation within the gravitational field of each observer. Moreover, it acts as if the mathematical apparatus used is real and not virtual.
One must be careful with the concept of reality, because for now, we have never seen a number walking down the street.
If we know all relations between the variables of the model, why we do not use this knowledge to create a stable system of units that would allow an intuitive vision of reality? What interest is there in not allowing an understanding of anything?
We have already commented on the definition of a second if we know how gravity affects atomic clocks, why the definition of a second does not include the velocity and the gravitational field intensity in the set of conditions for the clocks.
The Theory of Relativity besides being incorrect is the least scientific physics theory we could imagine representing reality.
The theory of the ignorant observer
This example, together with that of the light balls, is one of my favorites.
The discussion is not serious because of General Relativity usually and especially, in this case, contradicts Special Relativity by establishing a preferred reference system. However, it will force the reader to concentrate and realize how easy it is to confuse with such inappropriate terminology. The experiment of the Abrujuela on simultaneity is similar and complementary.
Books about Special Relativity usually repeat this subject in various examples, but these have the same basic idea. Let us imagine a pair of inertial observers for t equals 0. One of them is in the center of a train wagon, which is moving at a speed that is neither fast nor slow. The other inertial observer aligns at the station with the first one.
Just at that moment, a pair of lightning bolts fall on both ends of the wagon –we know it because we are setting the example, if not it would be difficult to know it.
The inertial observer at the station –let us say that he is the manager of the station– is in an inertial system fixed to the platform. This observer will see both bolts at the same time, because the distances from where they fell to him are equal, as he knows the speed of light is always the same –he had studied it just beforehand–, he deduces that the bolts are simultaneous.
We are going to suppose that this inertial observer is intelligent –and we know he is the manager or something.
The inertial observer who is on the wagon, director of the wagon, is in an inertial frame fixed to the wagon. Because the wagon is moving, he perceives the bolt that fell with a jolt, sorry, we mean the bolt that fell on the front of the train first, since he is moving towards that point.
Science experiment 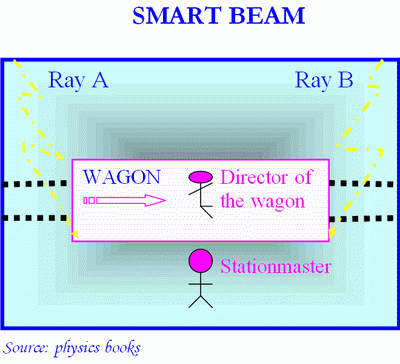
As he notices that both bolts fall with a small temporal gap –he had saucer eyes, like owls–, and because the speed of light is constant –he had also studied it–, he deduces that the lightning bolts did not fall simultaneously.
The conclusion of Einstein’s orthodox Special Relativity: two occurrences that are simultaneous for one observer are not for another inertial observer who is moving with regard to the first.
Our conclusion: following the scientific method and common sense, we can consider this observer ignorant. He could have taken into account the time it took to receive the information of reality and his displacement during that time, to give him an idea; that would be the rational thing to do. Wouldn’t it? After having studied it and everything!
Thunder and lightning! We do not want to imagine what he would have thought after hearing the matching thunder, for the time difference between them would be even higher, and it would probably cause him mental contradictions with the different simultaneities outlined.
Another thought situation could occur if two lightning bolts fell, but one of them fell on the ignorant observer. In this particular case, given that for this observer time stops indefinitely, he would think that all subsequent lightning bolts in the universe would be simultaneous. Then we could call him the enlightened observer.
The first observer was awesome, because he realized that the lightning bolts fell just on the little ends of the wagon, despite having seen one behind the wagon and the other some way in the front –he must’ve had eyes like an eagle–. There is a rumor that he was the little red dwarf from Venus.
As always, the clever neuron is lifting up its little dendrite to ask, so what would have happened if we had switched the observers?
