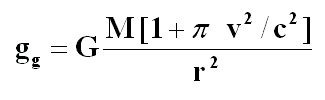Anomalous precession of Mercury’s orbit perihelion

IV.b.3. Celestial Mechanics and Planet Mercury’s orbit

If the prediction of Einstein’s General Relativity about the curvature of light is the most striking and spectacular one, due to its verification with the eclipse of 1919, explanation of precession of the perihelion of Mercury’s orbit –deviation from Newton’s Celestial Mechanics– is the most effective one thanks to its quantitative nature.

However, let us remark that in 1898 Paul Gerber explained this precession before relativistic physics with the same exact formula.

Astronomers had observed a deviation –unexplained by any known factor– of 43.1” of arc (43 arc seconds) in 100 years in the axis of the planet Mercury’s orbit. This deviation is to what refers precession of the perihelion of Mercury’s orbit, although in a strict sense, total precession –sum of explained and not-explained precession– is quite a lot bigger. Non-explained precession of Mercury’s orbit is about one ten-thousandth of a degree per year.

Using sophisticated field equations of relativistic mechanics, Einstein arrived at a figure very close to 43” arc seconds of the precession of Mercury’s orbit, not explained by Celestial Mechanics. See the webpage of mathpages* regarding the anomalous precession of Mercury’s orbit as explained by General Relativity.

It is not surprising that, given adjustment to orbits of the planets obtained by General Relativity, relativity as a whole would end up accepted, in detriment of other less adventurous alternatives. It is unquestionable that field equations of Einstein’s General Relativity contain some valid behavioral rules of nature, though they may hide in their mechanisms of conduct and calculus. Of course, we could say the same about Paul Gerber original ideas.

Let us now look to see if the Laws of Global Gravity also explain the precession of the perihelion of Mercury’s orbit.

Global Gravity Law

The expression for gravity acceleration –taken from the formula of the Global Law of Gravity– provides us with desired results on the angular deviation and the normal component of acceleration or centripetal acceleration.

To know total angular deviation in one revolution or the orbit of Mercury, we only have to substitute variables for their values. Acceleration *gg* should represent both the gravity force due to centripetal acceleration corresponding to Newton’s law and Merlin effect –second component of the atractis cause in Global Gravity Law.

That is, *g_g* will be the normal component of the acceleration or centripetal acceleration, which will cause a complete revolution of the planet in its orbit and observed precession for the period *T*.

This period *T*, by its definition in trigonometry, would cause precisely one complete revolution according to Newton’s Law of Universal Gravitation. As Kepler’s laws showed from orbits of the planets of Celestial Mechanics, we know that a perfectly elliptical orbit would result from the inverse-square law –of the radius.

Don Magufo revealed a fast way to estimate centripetal acceleration or normal component of the acceleration with intuitive mathematics. But before continuing, we would like to review the necessary data to carry out calculus, plus the unnecessary *v*, which are:

G = Universal gravitational constant = 6,67266 * 10^-11 (m² N / kg²)
c = Speed of light = 2,99792458 * 10⁸ (m/s)
M = Mass of the the Sun = 1,98892 * 10³⁰ (Kg.)
r = Average radius of Mercury’s orbit = 57,9 * 10⁶ (m)
T = Mercury’s orbit period = 7,60018 * 10⁶ seconds = 414,9378 orbits in 100 years
v = Average speed of Mercury = 47948,31 (m/s)

For empirical verification of planet Mercury’s dynamics we have the following steps:

• Circular planetary orbit

  We have chosen a circular orbit case to simplify calculus because the play of gravity forces would continue to exist and eccentricity of planet Mercury’s orbit is quite low. It is enough for our purpose here.

• Calculus of revolutions per period with Newton’s Law of Gravity

  The formula for the Global Gravity Law equals the sum of two components:

  

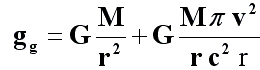
  The first term on the right-hand side of the equation is the gravity of Newton’s law or centripetal acceleration. In one period, it produces an angular variation of one revolution –or 2π radians.

  So then, if we multiply and divide it by *v²*, and substitute *v²/r* for the normal component of acceleration or centripetal acceleration *an*, we will be left with:

  

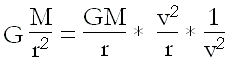
  Recalling that orbital speed is the square root of *GM/r*, we have:

  

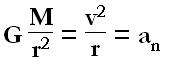
  v T = 2πr

  w T = 2π

  v / r = w

  a_n / v = w

  a_n T / v = T (v²/r) (1/v)

  = Tv/r = wT =

  = 2π Radians Q.E.D.

  The normal component of acceleration *an* is related to change in the direction of velocity with time. If we evaluate this change for each *m/s* –dividing it by *v*– and we multiply it by period *T* –number of total seconds in one revolution–, it will give us through trigonometry *2π* radians –one entire revolution of planet’s orbit.

  Analytically, above reasoning would be:

  We could verify it by carrying out calculus using the value of the average speed of the planet Mercury. One entire revolution has 2π radians or 360 degrees, each degree has 60’ minutes and each minute has 60” arc seconds.

  G			6,67266E-11
  Mass of the Sun	1,98892E+30	GM	1,32714E+20
  Average radius	5,79000E+10	an= GM/r²	3,95876E-02
  Average v	4,794831E+04	an / v = w	8,25631E-07
  Revol. 100 years	4,149378E+02
  Period T	7,60018E+06	w * T = 2 π	6,27494E+00

   

• Calculus of revolutions per period due to the Merlin effect

  We are looking for the second term on the right-hand side of the equation for the Global Gravity Law, given that it is the centripetal acceleration caused by Merlin effect –double attraction provoked by kinetic energy. This centripetal acceleration will cause the precession of the perihelion of Mercury (ppm) –or of any planet’s orbit in Celestial Mechanics– if we estimate it for the entire period, considering how we did it previously with *a(n)* to calculate the *2π*radians.

  According to Don Magufo, the intuitive integral of the differential equation not set out can be directly resolved if, once *v²/r* is substituted by *a(n)*, we use its value for a whole period, which, as we have just discussed above, in terms of trigonometry will be *2π*.

  In strict terms, it is enough to mention that formal integral, regarding the period, of centripetal acceleration, resolves without any problem; since speed, centripetal acceleration and rest of variables are all either constant or independent of time, due to simplification to a circular orbit of the planet Mercury. For this reason, it coincides with the simple calculations of trigonometry, as integral to *dt* is 1.

  So it remains that:

  

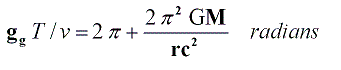
  Therefore, the precession of the perihelion of Mercury in radians will be:

  

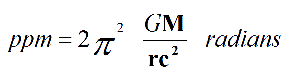
  Value of ppm obtained using above equality, derived from Global Physics, is 43.08” arc seconds every 100 years, as following table shows:

  G			6,67266E-11
  Mass of the Sun	1,98892E+30	GM	1,32714E+20
  Average radius	5,79000E+10	an= GM/r	2,29212E+09
  c²	8,98755E+16	GM / r c²	2,55033E-08
  π	3,141592654	π GM / r c²	8,01210E-08
  2 π Radians/revol.	6,283185307	ppm = 2π² GM / r c²	5,03415E-07
  Revol./100 years	4,14938E+02	radians/100 years	2,08886E-04
  Arc sec/radian	2,06265E+05	Arc sec/100 years	4,30858E+01

  * * *

Let us recall that, if in this formula we replaced *2π* by *6*, it would give us the formula obtained by Paul Gerber in 1898 and Einstein in General Relativity, regardless of the eccentricity, as mentioned in the book Theory of Relativity, Elements, and Criticism.

For Earth, Einstein’s General Relativity gives a value of 3.8 arc seconds; Global Physics gives 4.02, and the observed value is 5 arcs seconds according to Mathpages mentioned website.

 

Average radius 106 km	Planets	Radians	Revolutions 100 years	Total radians	Precession arc second
					Observed	RG	GF
57,90	Mercury	5,03415E-07	414,93780	2,08886E-04	43.10	42,9195	43,08581
108,20	Venus	2,69387E-07	162,60160	4,38028E-05	8.65	8,6186	9,03498
149,60	Earth	1,94838E-07	100,00000	1,94838E-05	3,85	3,8345	4,01882
227,90	Mars	1,27897E-07	53,19150	6,80303E-06	1,36	1,3502	1,40323
778,30	Jupiter	3,74505E-08	8,43170	3,15771E-07		0,0623	0,06513
1427,00	Saturn	2,04259E-08	3,39440	6,93336E-08		0,0137	0,01430
2869,60	Uranus	1,01574E-08	1,19030	1,20904E-08		0,0024	0,00249
4496,60	Neptune	6,48217E-09	0,60680	3,93338E-09		0,0008	0,00081
5900,00	Pluto	4,94029E-09	0,40320	1,99193E-09		0,0004	0,00041

Although there is no doubt both theories are good approximations –three if we include Paul Gerber–, or forms of looking at the same problem about the orbit of the planet Mercury, we must say they are mutually incompatible since same angular deviation would be doubly explained.

Moreover, they have different and contradictory principles, which will make unnecessary to resort to Occam razor. Also, other natural phenomena and physics experiments will help to tip the balance definitively.

With the Laws of Global Gravity, we have accurately explained the precession of the perihelion of Mercury's orbit, because of the Merlin effect in the interaction of Global Aether (gravitational - kinetic - mass) with bodies with mass.

In other words, the principle of equality between gravitational and inertial mass established by Newton and upheld by Einstein is vague and unnecessary, given that behavior of physical mass in its interaction with Global Aether is the same with or without a gravitational field, although there could appear different forces. However, in Global Physics, there is no need to stretch time and space to explain elliptical orbits of the planets.

Section Second Law of Newton of the book Physics and Global Dynamics studies in more depth differences between Newton, Einstein and Global Physics, which are due to fundamental changes in mass and acting forces.

Another experiments regarding planetary orbits are in page Gravity Probe B and Paradox of the last dolphin of the Global Astrophysics and Cosmology book.

To conclude, we would like to point out that not once has been abandoned the non-curved geometry of Euclidean space, despite planet Mercury’s orbit, and that Global Physics is consistent with absolute time.

 

 

♦

When Einsoder finished the Web page,
he happily went to tell it to Prinspick, who said:

–Very good. And what did you do after that? –

Einsoder, hesitating a pit, dit:

– I started to play with marbles
thinking about number π.
Then, a pish girl appeared,
she threw herself at my pheet,
and opened her pleegs
staring at my piballs. –

And Prinspick exclaimed:

–That’s picorny! –