3.c) Correlations between Wechsler and Stanford Binet scales  

The preliminary analysis of correlations of the involved variables, including Wechsler and Stanford Binet scales, helps us to understand the intrinsic difficulties of the original model of intelligence, the reasons for its reformulation, and even the convenience of performing a simulation to confirm the model's goodness-of-fit.

The first surprise is the observation of low correlations not only between the Mother (M) and Father (F) variables with C (Children) variables, but also among children variables (Wechsler, Stanford Binet and others scales).

The variables of the children like Wechsler intelligence test and Stanford Binet scale correspond to same children at different times. And not only the correlations between the scales of Wechsler and Stanford Binet are not high but even between two IQ vectors of the same children and the Stanford Binet test.

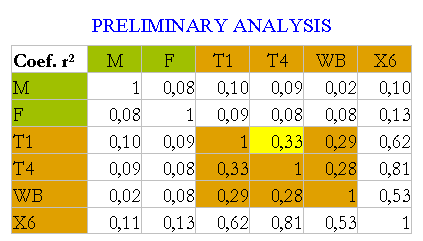
The coefficient r² = 0.33 is the largest one among the IQ variables of the children (Wechsler, Stanford Binet test and other test). With this perspective, it seems to be difficult to imagine that high correlations can be obtained between children and their parents.

At the beginning, the previously mentioned grouping of values had still not been considered. Taking into account these correlations, I thought about substituting the values considered to be very disparate, by their averages, but the different variables continued to show a low correlation.

These assessments of the low or not very high correlation between the children variables C (Wechsler, Stanford Binet test and other test) make us think that the measurements are not very homogenous because it seems that it is generally accepted that people's IQ remains fairly stable after 6 years of age.

Given that the averages of the chosen variables were not equal, I decided to standardize them for a suitable calculation of the variables X3 and X6 (Wechsler, Stanford Binet test and other test). This way of calculating is necessary in order to avoid distortions and any additional problems, considering that we are not trying to study the evolution or generational increase in IQ. This fact has been proved and accepted, although different explanations on the matter have been proposed. In our case, the data produced an average, of the different IQ data set of the children, 10% above the average of IQ data set of the mothers and fathers.

A consequence of the lack of IQ measurement precision is the impossibility to make a discretionary selection of 50% of the sample to isolate the cases in which supposedly the gene with less potential dominates; in agreement with the statistical model initially proposed.

It is as if we had several Photos or pictures of each child that, sometimes, do not look alike; but perhaps, altogether, they could give us a relatively clear image of the child.

Other factors that could contribute to the mentioned impossibility are: the multifunctional character of human intellect and that, as the model depicts, the IQ of the child can be inferior to the smaller of the two parents when the latter is not entirely included in the greater one. This aspect will be discussed in more detail in other chapters.

As shown, this preliminary analysis has allowed us to recognize the difficulties in obtaining satisfactory results and that it is better to use original values since their manipulation, although objective, does not improve the results significantly.

Also, I have used centred variables, that is to say, one with smoothed tails due to a limitation of a 10% deviance from the average (T1-d) and variables X3 (Wechsler, Stanford Binet test and other test) and X6 (Wechsler, Stanford Binet test and other test), which are average values of three and six original variables respectively.

The solution will come with the model of intelligence reformulation and a bit of imagination.

4. Individual model of intelligence  

4.a) Mendelian genetics significance  

The formulation of the empirical research model made in the GTCEL book is validated in this statistical study.

--- GTCEL MODEL WITH MENDELIAN GENETICS---

The proposed model for empiriral research assumes the following hypotheses:

• Evolution with external verification of the genetic information transmitted for the studied capacity.

• Existence of a function x that measures the different potentials from this capacity.

In order to facilitate the understanding of the model and its statistical analysis, we are going to choose the controversial subject of heritability of intelligence. Numerous studies based on individual IQ or intelligence quotient measurements exist.

Intelligence is normally measured with the generally accepted IQ tests, although many authors doubt these measurements and even the unique concept of intelligence. Nevertheless, the IQ refer to the relative position defined by means of a standardised function x (I) of the statistical distribution of the IQ studied for the validation process of this function.

The empirical research and studies have some contradictory conclusions, whereas in studies with identical twins a correlation of 80-85% is reached, for other types of kin relations, decreases to a 30%. For me, the conclusion is that intelligence is inherited as high correlation between identical twins demonstrates.

The low correlation in the rest of the cases is due to the incorrect definition of the form in which the inheritance is transmitted in agreement with the exposition of the GTCEL and mendelian genetics.

The figure shows the shape of the Normal function x (IQ), which we are going to use. For each IQ value, the function indicates the accumulated probability that the IQ of the population is the same or less than the IQ reference value.

For example x (100) = 0.5 and the opposite function x_inv (Prob) = IQ, that means, x_inv (0.5) = 100.

The statistical IQ data set includes de variables of Wechsler and Stanford Binet scales that have Normal distribution with standard deviation of 15 and 16 respectively.

The result of the combination of the four genes in agreement with mendelian genetics significance will produce four different possibilities or cases. The mathematical expected average of the capacity of the new individual in agreement with the GTCEL will be the sum of the expected averages of each one of the cases weighed by their probabilities.

ECdescend. = P(D1) C(D1) + P(D2) C(D2) + P(D3) C(D3) + P(D4) C(D4)

Considering that the assumption of verification of the received genetic information, assumed by hypothesis, says that the dominant gene will be the one with less capacity, at the most it would only be possible to be expressed the potential of that gene in his integrity .

Despite this consideration, in the empirical research I will suppose, for simplification, that it is contrasted in its totality, since it is reasonable that for a specific capacity the greater gene contains practically all the information of the smaller gene plus an additional part.

Another important aspect is that by hypothesis, the more powerful gene (or the part of the genetic information that is associated to the studied capacity) of each ancestor cannot be measured in a empirical research since it is not expressed in its integrity because only the contrasted part will be expressed.

For that reason, it is necessary to estimate its size as precisely as we can. If we always worked with probabilities of the central value of its mathematical expected average, when calculating the correlation between dependant variables and independent ones, the errors would tend to compensate.

Although the most powerful gene could also be measured, it would remain the problem of the randomness of the Mendelian inheritance.

Once the data of the sample studies of the empirical research is available it will be possible to analyse the correlation between the explanatory variables defined by the model with the explained ones.

The present model is a simplification for its presentation. For example, surely it could be necessary to include:

• The internal improvement of the genetic information in each generation that could exceed 10%. In any case, it is possible to make preliminary studies for its estimation and later inclusion.

• The afinity filter, related to the lack of contrastation of the intellectual power in its totality as mentioned above.

• Another factor, althought not clear, could be the effect of the sexual selection related to the correlation of the intellectual power between genes of both progenitors.

Another important aspect is the possibility of calculating the correlation of the IQ inheritance with half the cases, only those where the less porwerful of the four genes is indeed the dominant gene, that is to say, that the partial correlation of that 50% of the cases would have to be around 80-90% and the expected value should be centred and with a very small variance.

--- --- ---

Let us remember that this last possibility has been rejected in our preliminary analysis. On the contrary, as I mentioned in another paragraph, it will be necessary to complicate the model to obtain better estimations, (although now I would dare to say, more impressive). For example, the confirmation of the increase of 10% in each generation will be confirmed, as we will see later.

4.b) Results of the model of intelligence  

In the empirical research, when estimating the model of intelligence with the method of the ordinary least squares, I am not interested in obtaining the value of the parameters; on the contrary, I am looking for the goodness-of-fit of the estimation, that is to say, its correlation coefficient (r) and its squared or determination coefficient (r²); they represent the relation between the explained variance and the total variance.

Surely, when the model of intelligence of this empirical research is well established, the parameters' values will begin to be useful.

As expected, the table shows the poor results of the simple model of intelligence. On top of the talbe, there are the six variables, the three original variables of the children T1(Stanford Binet scale), T4, WB (Wechsler scale) and the centred variables, T1-d(Stanford Binet scale) corrected with the extreme values, (Wechsler, Stanford Binet test and other test) and X6 (Wechsler, Stanford Binet test and other test).

Parents' variables are function R, M1F1, (M+F)/2 and M & F; where M1F1 is the vector produced by the smaller values of M or F for each family. The M & F correlations are attained using the ordinary square minimums method with C variables (Wechsler, Stanford Binet test and other test) and with both ancestors simultaneously.

The best result is obtained when simultaneously using the variables M and F. Nevertheless it continues being very low and quite below the inferior level of generally accepted dependency, which is established within the range of 0.35 - 0.80 by previous studies on twins.

A correction due to the degree of kinship between expected and observed correlations for determining the hereditariness degree cannot be applied since the expected correlation between parents and children is unknown.

Even if the corrected results were 50%, they would continue being very low, although they would be around the indicated inferior level of 0.35

To explain these results, we can clearly deduce that there will be variations due to the Mendelian inheritance. Also, from the low correlations between C children variables themselves, we realise that the IQ values incorporate great deviations due to their measurements, the particular intelligence test used, and the manifestation of the intellectual potential or brainpower due to fatigue.

At this stage, I decided to carry out the analysis in groups with the hope that these differences would be compensated and, consequently, increase the correlation of the model of intelligence.