variable X3 (q073) variable X6 (q076) sexual selection & X6 (q077)
STATISTICAL GRAPH
Each vertex or round point of the Globus model graph represents the Global Multidimensional Correlation Index (GMCI) corresponding to the correlation graphs of the Global model between the dependent variable R°, or the M&F, with the dependent variable or variables; all arranged according to the * M1F1 ° arrangement criteria.
Displayed in the horizontal axis is the evolution percentage which in every case has been associated with the intelligence quotient (IQ) variables, M or F, in the generation of the variables R° and * M1P1°, which are the only ones that are affected by these changes in the parameters of evolution (°).
See the methodology of the statistical abstract for more details
STATISTICAL STUDY COMMENTS
1. General statistical significance
The considerable increase of the correlation for the estimation of homogenous groups is not due to the reduction of 68 to 5 or 4 degrees of freedom, since the estimation with non-homogenous groups, without previous rearrangement, has the same degrees of freedom and the correlation even lowers concerning the sample without grouping.
In general, the model of the genetic evolution of intelligence (Mendelian genetics – Conditional intelligence – Global Cognitive Theory) adjusts perfectly, showing an r² superior to 0.9 in several cases. Bearing in mind the tendency to increase the goodness of fit with the size of rearranged groups, we could assume it would be over 0,9 in almost all the cases for grander groups within a more significant sample.
2. Globus Model and Sexy Globus Model - Sensitivity analysis
Considering that internal evolution parameters ( ° ) will affect the objective function °R and variable *M1F1° of the sample's previous rearrangement, the effect on the correlations of changes in these parameters would allow us to see changes in the goodness-of-fit of the Global Model's specifications.
Using sensitivity analysis of these parameters in the Globus Model will show us their optimal magnitude. This type of analysis reconfirms the Global and Social models of the evolution of intelligence.
The analysis with original variables is not as conclusive as with centered variables; the later generate more precise results.
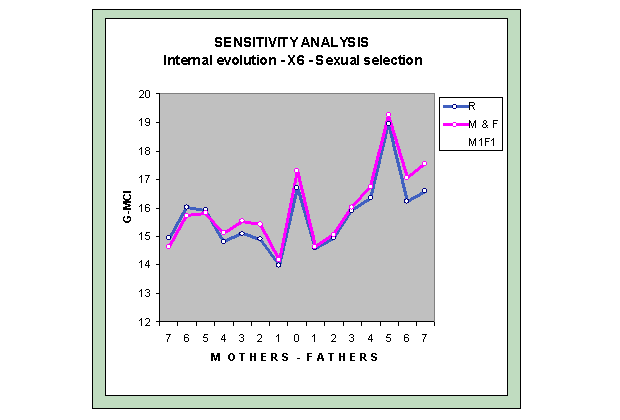
The graph shows the best adjustment is for a value of 5% for each of the parameters of internal evolution, direct and indirect.
The complexity of the model is very high due to the existence of sex-linked genes or chromosomes. Nevertheless, the Global Model can detect a different effect. Even more, it will be able to sense the effect of sexual attraction on mate selection.
A good way of understanding the analysis of the Sexy Globus Model is to view the three graphs and concentrating in the reason of the improvement of the results.
The Globus Model is proof of evolution, and on the other hand, it should be challenging to justify an increase of 10% in intellectual abilities with the classical theory of Darwin. On the contrary, the statistical analysis carried out is entirely consistent with the general theory of the Conditional Evolution of Life.
3. Significant comments on this particular graph
The dependent variable is X3 of the children with the hypothesis of sexual selection.
It could be said that the graphs are speak for themselves. This graph shows the optimal goodness-of-fit is achieve with a internal evolution parameter of 5% of the masculine IQs
The optimal percentage is clearer with the variable X6 of the children with the hypothesis of sexual selection than the other variables.
Also, the behaviour of variable R ° is closer to M & F as we have seen in previous cases.
The synchronization of R ° and M & F with the hypothesis of sexual selection and X6 confirms the power of R ° to detect the effects of M & F in relation with the heritability of intelligence.