STATISTICAL GRAPH
The title of each graph of the statistical study indicates the parents' variables (R or M & F) to which the correlations relate. Each point of the colored lines represents the correlations with the observational C variables of the children.
Likewise, the variables of unknown order, formed by the different groups of 1 to 10 values from the 70 IQ values of each parent and children variables, appear on the left-hand side of the graph. The criteria order of the groups of 1 to 10 values located on the right-hand side is the variable mentioned at the bottom of the graph.
Indeed, there is an almost instantaneous perception of the exactitude of the particular specification of the statistical study; each graph shows sixty coefficients of determination (r²) highlighting the global and underlying relations of the involved data set.
See the methodology of the statistical abstract for more details
STATISTICAL STUDY COMMENTS
1. General statistical significance
The considerable increase of the correlation for the estimation of homogenous groups is not due to the reduction of 68 to 5 or 4 degrees of freedom, since the estimation with non-homogenous groups, without previous rearrangement, has the same degrees of freedom and the correlation even lowers concerning the sample without grouping.
In general, the model of the genetic evolution of intelligence (Mendelian genetics – Conditional intelligence – Global Cognitive Theory) adjusts perfectly, showing an r² superior to 0.9 in several cases. Bearing in mind the tendency to increase the goodness of fit with the size of rearranged groups, we could assume it would be over 0,9 in almost all the cases for grander groups within a more significant sample.
2. Social Model and original variables
The results of the model following Mendelian genetics and the general theory of Conditional Evolution of Life (CEL) are surprising, which can be observed both in the graphs and in the table resume. The model sensitivity to the arrangement criterion will allow reaching some crucial conclusions.
Also, the objective function R is almost as powerful as variable M of mothers and F of fathers together, which means it contains the actual rules o the evolution of intelligence.
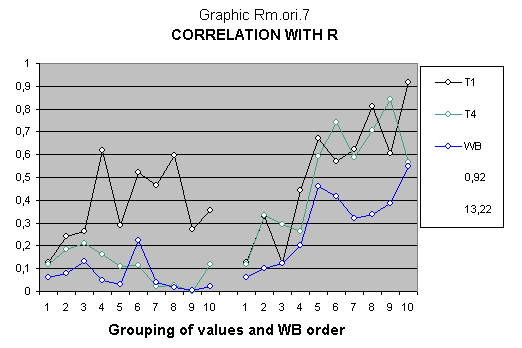
3. Significant comments on this particular graph
As you can clearly see by its form, two dependent variables of the children T1 and T4, analyzed in the model, behave in a very similar way to the progenitors' explanatory variable R
In fact, the determination coefficient r² is bigger than 0,8 for both variables of the children T1 and T4 which is a significantly high value for the generally accepted value in other works about intelligence heritability.
The general multidimensional correlation index (GMCI) is 13,22 which is relatively low in the whole EDI study.
The WB variable of the children differs from the other two variables of the children, but this seems to be due to the fact that it is also used as an arrangement criterion. Even though it seems contradictory in principle, this effect is due to the fact that the statistical deviations of this variable have a double effect, they not only disturb the correlation as a dependent variable but the dependent variables as well by being used as an arrangement criterion, which creates greater distortions.
The highest determination coefficient r² of this graph is 0,92 which is a high value for this type of research.